An Efficiency Comparison between Hash Maps and Bloom Filters in C++
Monika Kanphade - November 9th, 2023
What is a Hash Map?
Hash Maps are a data structure resembling a dictionary, storing elements in a key-value fashion. \ They use buckets to store values in unique keys determined by hash functions. \ The keys are unique indexes into the data structure that allow efficient retrival of a certain value from the lookup table.
How does it work?
Hash Maps work like a dictionary storing key-value pairs. The specific bucket that the key-value pair \ gets mapped to is dependant on the Hash Function used to calculate it.
For example, if you wanted to store numbers efficiently, one hash function you could use to store them \ in seperate buckets would be to differentiate based on the digit in the tens place of each number, \ resulting in buckets for digits 0-9.
- The number 13 would go in Bucket 3
- The number 27 would go in Bucket 7
- The number 5 would go in Bucket 5
- The number 147238674 would go in Bucket 4
Retrieval or search of the values is based on running the key through the Hash Function and determining if the \ exact value is present in the location returned.
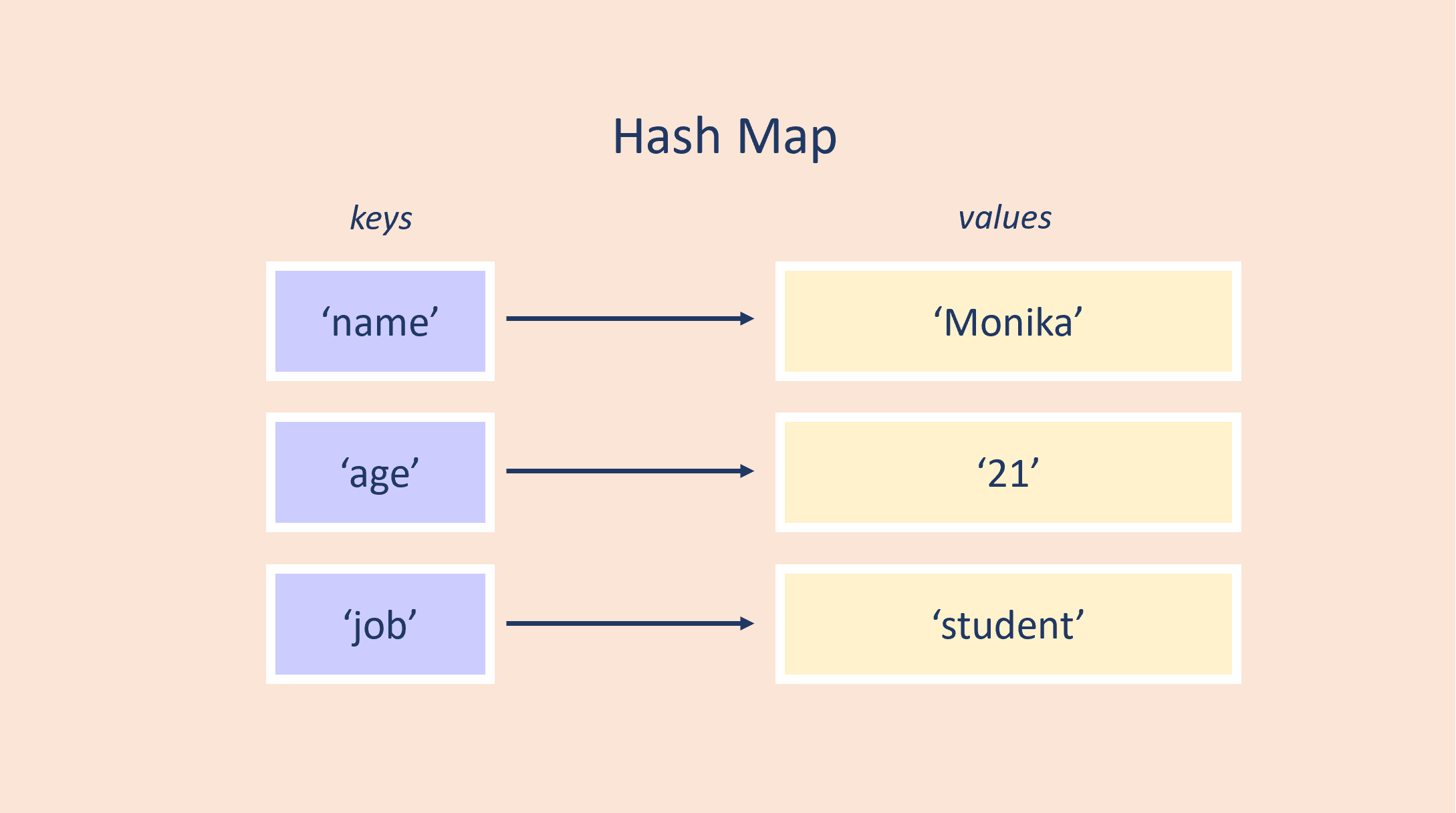
Implementation in C++:
#include <iostream>
#include <unordered_map>
#include <string>
int main() {
// Initialization of Unordered map (Hash map)
std::unordered_map<std::string, std::string> hash_map;
// Inserting values by using [] operator
hash_map["name"] = "Monika";
hash_map["age"] = "21";
hash_map["job"] = "student";
// Traversing an unordered map
for (auto pair : hash_map)
std::cout << pair.first << " " << pair.second << std::endl;
}
What is a Bloom filter?
Bloom filters are a probabalistic data structure that determine if a given key has been seen by the structure before. \ Oftentimes, they are used to determine data that has not been seen yet for particularly large datasets, however, \ the larger the dataset the more likely the bloom filter is to report a false positive (i.e. claiming that a key has been \ seen before when it hasn't).
How does it work?
A Bloom Filter works similarly to a Hash Map, with some distinct differences. It works like a dictionary, however, \ instead of storing the exact key-value pairs, it stores a numerical representation (usually a bit representation) \ of the value. It determines what bits are to be set (in a sequence of n bits determined at initialization of \ the Bloom Filter), by one or more Hash Functions.
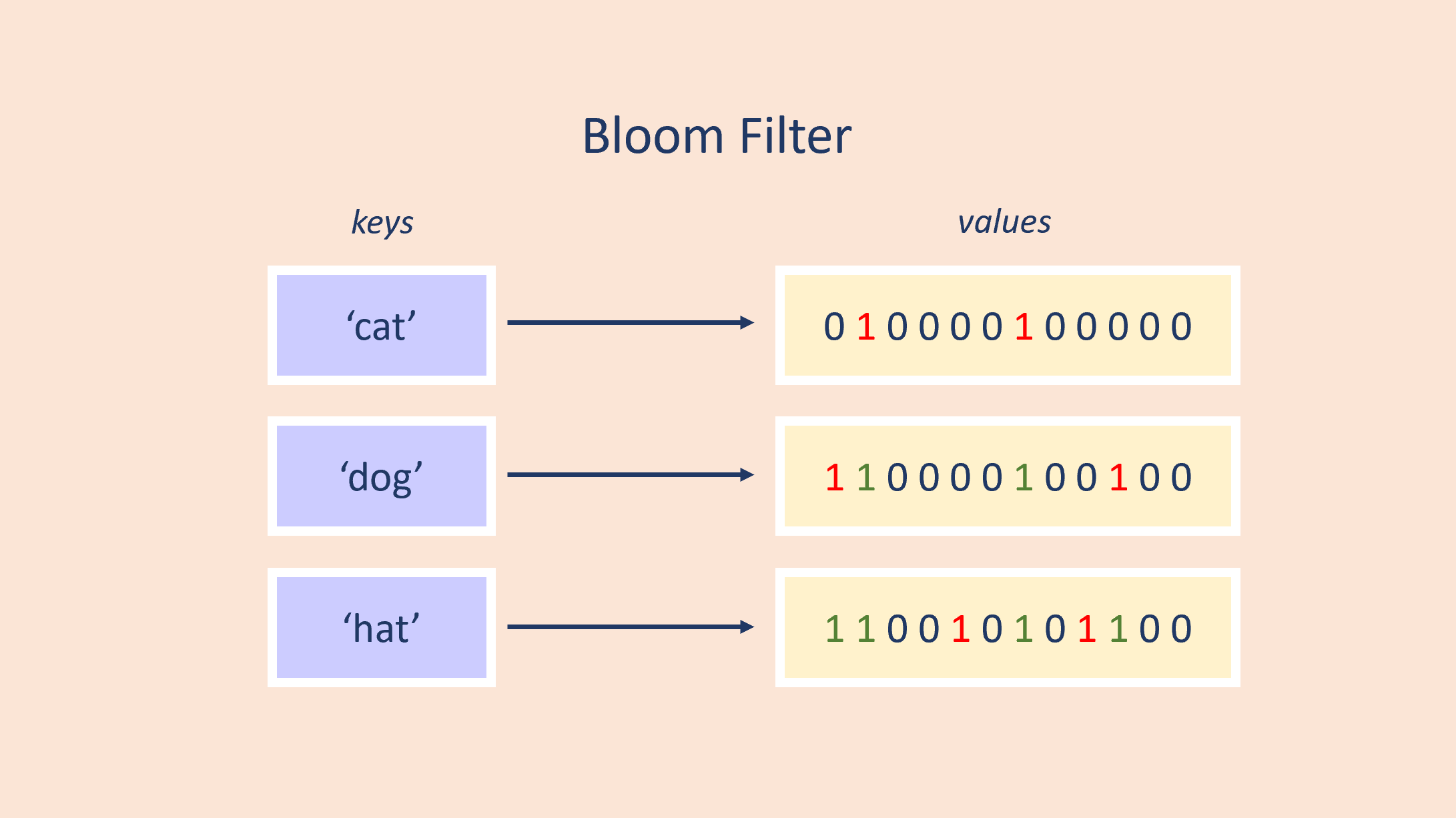
For example, using keys from the image below, we can initialize the Bloom Filter's length n to 12 bits, \ all set to 0. According to a Hash Function (I won't specifiy the details of how it works for simplicity's sake), \ if I input the word 'cat' the function might output bits 1 and 6 to be set (starting from 0).
- The word 'cat' sets bits 1 and 6
- The word 'dog' sets bits 0 and 9
- The word 'hat' sets bits 4 and 8
In order to check whether one of these words is present in the Bloom Filter, you would simply evaluate the Hash Function \ for that word and if all the calculated bits are set to a 1, then it has most likely been seen.
I say most likely under the pretense that the calculation may be a false positive. The idea of false positives comes \ from the idea that the more bits set, the less unique the encoding of the word becomes.
In our example, say you want to know whether the word 'hog' has been seen or not. You run it through the Hash Function \ and it calculates that bits 4 and 9 must be set to 1 in order to return True. Well, looking at our Bloom Filter, \ we can say that bits 4 and 9 have been set to 1, but not necessarily together. They were set under the context of other \ words being seen. This pattern would mean that the Bloom Filter returning True for the word 'hog' would be a \ false positive as we never actually saw it.
Some ways to reduce the number of false postives appearing in your Bloom Filter search would be to increase the \ size of the array of bits, increase the number of Hash Functions used to create more unique outcomes in which bits to set, \ or reduce the size of the data being input.
Implementation in C++:
From: https://github.com/ArashPartow/bloom/blob/master/bloom_filter.hpp
#include <iostream>
#include <unordered_map>
#include <string>
int main() {
// Initialization of Bloom filter
bloom_parameters parameters;
parameters.projected_element_count = 10; // number of elements to insert
parameters.false_positive_probability = 0.0001;
parameters.compute_optimal_parameters();
bloom_filter bloom_filter(parameters);
// Inserting values using .insert() function
bloom_filter.insert("cat");
bloom_filter.insert("dog");
bloom_filter.insert("hat");
// Check if Bloom filter has seen a unique key
std::cout << bloom_filter.contains("cat") << std::endl; // True
std::cout << bloom_filter.contains("bat") << std::endl; // False
}
Behind the scenes
Space Complexity:
Hash Map:
Hash maps are oftentimes represented as an array containing n key-value pairs. The size of the array is dynamic, \ but the space complexity may also depend on the size m of the items it is storing. Different data types have \ different sizes.
- Best case: O(n) - When items stored in the array are type int, bool, etc.
- Worst case: O(nm) - When items stored in the array are type string, objects, etc.
Bloom Filter:
Bloom filters are also represented by an array, however, instead of containing the literal representation of the keys \ themselves, it contains a set number m of bits then can be set upon seeing a unique key. This makes them very \ space-efficient as the size is not dynamic.
- Best/Worst case: O(m) - The size of the bit array
Time Complexity:
Hash Map:
The time it takes for a Hash map to INSERT, DELETE, and SEARCH for data depends on a multitude of factors, \ such as the size of the buckets and whether they hold a singular item, and what the Hash function being used to map \ key-value pairs looks like. Collisions may increase the time complexity but can be prevented by a good hash function \ allowing uniform data distribution.
- Best case: O(1) - When a key maps to a single value
- Worst case: O(n) - When a key maps to multiple values
Bloom Filter:
The time it takes for a Bloom filter to INSERT and SEARCH for data depends on the number k hash functions \ implemented. Everytime a key is inserted into the bloom filter all hash functions must be applied for the key to \ attain its mapped bit values. When searching, the Bloom filter simply checks if all hash functions return a 1, \ indicating that bit was set.
- Best/Worst case: O(k) - The number of hash functions implemented
Code Review
Insertion Tests:
// Testing hash map insertion
for (int i = 0; i < 10000; i++) {
hash_map[i] = i;
}
>>> Time Elapsed: 14007 microseconds
// Testing bloom filter insertion
for (int j = 0; j < 10000; j++) {
bloom_filter.insert(j);
}
>>> Time Elapsed: 1926 microseconds
Bloom filter wins!
Search Tests:
// Testing hash map search
for (int i = 0; i < 10000; i++) {
hash_map.find(i);
}
>>> Time Elapsed: 1008 microseconds
// Testing bloom filter search
for (int j = 0; j < 10000; j++) {
bloom_filter.contains(j);
}
>>> Time Elapsed: 1996 microseconds
Hash map wins!
Space Complexity Tests:
// Insert 3 items into hash map
hash_map["name"] = "Monika";
hash_map["age"] = "21";
hash_map["job"] = "student";
std::cout << sizeof(hash_map) << std::endl;
>>> Size: 56 bytes
// Insert 3 items into bloom filter
bloom_filter.insert("cat");
bloom_filter.insert("dog");
bloom_filter.insert("hat");
std::cout << sizeof(bloom_filter.size()) << std::endl;
>>> Size: 8 bytes
Bloom filter wins!
Summary
Overall, Bloom filters and Hash maps have their unique properties can allow the user an advantage in certain situations. \ Say you wanted to keep track of a large dataset for which you did not have enough memory to hold the individual instances \ of the data, a Bloom filter would be a perfect solution if the possibility of false positives wasn't an issue. However, \ if you needed to ensure accuracy about whether something is in the data and require some form of deletion, a Hash map \ would be the way to go as Bloom filters have trouble implementing a way to delete values.